Basic SIMD

By now, we have largely resolved the slicing-induced performance bottleneck that plagued our initial naive simulation code. But as we have seen in the introductory chapters, there is still much to do before our Rust code puts hardware to good use.

In particular, we are not using SIMD yet, for reasons that will become clear once you realize that we are effectively computing one tiny dot product per output concentration value. As you know from earlier chapters of this course, compilers cannot translate naive dot product computations into efficient SIMD code, we must perform the translation for them.

This is the first thing that we will need to fix in order to use our hardware more efficiently.

Picking a granularity

This computation is complex enough that there are actually two different ways to vectorize it:

1. We could try to internally vectorize the computation of a single (u, v) concentration value pair. The diffusion gradient computation, which is basically a dot product, would be an obvious candidate for vectorization as we already know how to compute SIMD dot products.
2. On each iteration of the loop, we could try to compute not just one pair of concentration values, but one full SIMD vector of concentration values for each chemical species. Basically, anywhere the current code manipulates a single floating-point number, the new code would manipulate a full SIMD vector of floating-point numbers instead.

Are there any reasons to prefer one of these two options over the other? Indeed there are:

• Option 1 only lets us vectorize a subset of the computation, while option 2 lets us vectorize the full computation. Because Amdhal’s law is a thing, this is an argument in favor of option 2.
• Option 1 involves performing SIMD horizontal reductions (going from a SIMD vector of inputs to a single floating-point output) in a tight loop. In contrast, option 2 involves no horizontal reduction. Because horizontal reductions are slow, this is an argument in favor of option 2.
• Option 2 only makes sense if the entire computation is done using SIMD. This will consume more SIMD execution resources (CPU SIMD registers, etc) and make our life difficult in the presence of constructs that do not map well to SIMD like if/else and loop early exits. Therefore, on certain hardware architectures or for sufficiently complex code, only option 1 (fine-grained SIMD) may be available.

In this school, we are using x86 CPUs, which perform scalar floating-point operations using the same CPU resources as SIMD operations. Therefore, switching to SIMD will not change the CPU resource usage profile, and there is no risk of blowing a CPU hardware budget that we used to fit in before.

And on the code side, our computation is simple enough that translating it to SIMD operations is not super-difficult. So overall, for this computation, option 2 (coarse-grained SIMD) is the clear winner.

Visualizing the goal

As it turns out, the simplest way we can go about introducing SIMD in this computation is to make our input and output windows wider, as we will now visually demonstrate.

Currently, we are jointly iterating over input windows and output values as in the following sketch…

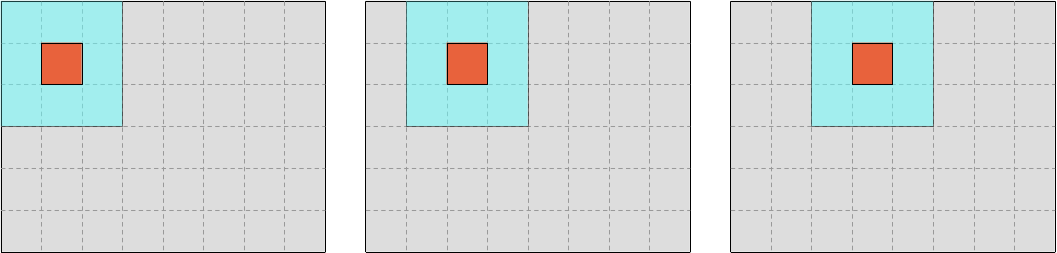
…where the gray rectangle represents the overall dataset, the blue square represents the location of the input values that we are reading at each step of the update loop, and the red square represents the location of the output value that we are writing at each step of the update loop.

Our goal in this chapter will be to instead iterate over wider (but equally high) input and output slices, where the output region is as wide as a hardware SIMD vector, and the input region follows by adding one data point on each side.

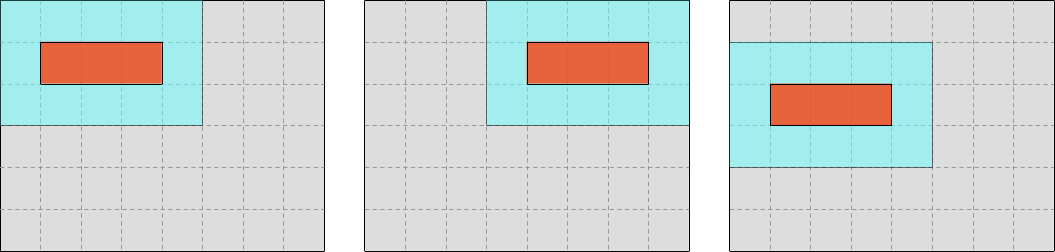
Once we get there, introducing SIMD will “just” be a matter of replacing each scalar operation in our algorithm with a SIMD operation that targets a SIMD vector starting at the same memory location.

Breaking the symmetry

This move to wider input and output windows is not without consequences, however. It breaks the symmetry between rows and columns that has existed so far in our computation, allowing us to perform 2D iteration over the dataset with a single, 1D-feeling loop.

Now we are going to need an outer loop over lines of output…

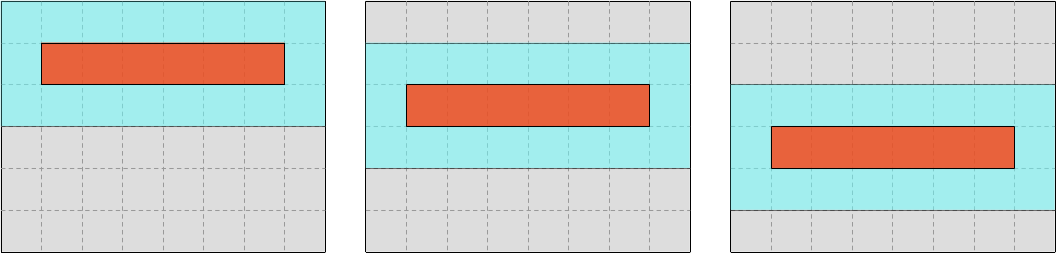
…and, under that outer loop, an inner loop over SIMD vectors within each line.

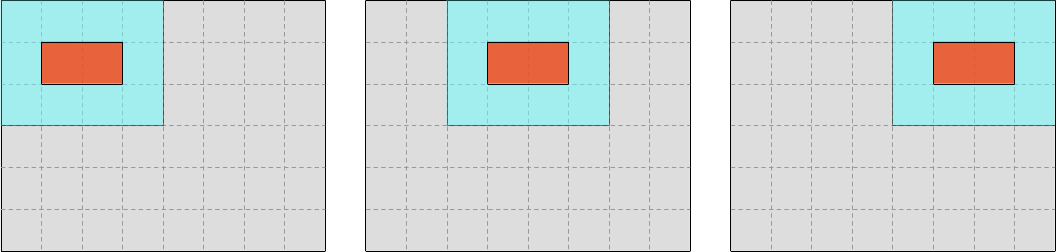
We are also going to need to decide how to handle the case where the number of output elements within a line is not a multiple of the SIMD vector length:

1. Do we simply forbid this to keep our code simple, at the cost of making users angry?
2. Do we handle the remaining elements of each line using a scalar computation?
3. Do we start by slicing up a “regular” part of the computation that has all the right properties for SIMD, processing the rest (including the edges of the simulation domain) using a more general but slower scalar implementation?

There is no single right answer here, and the right way to go about this will depend on the technical and political specifics of the software that you are writing. But option 3 is a good tradeoff if you are unsure, and may therefore be a good starting point.

The “easy” part

We will now start implementing a subset of the update loop that only works on the part of the simulation domain that is easy to handle using SIMD.

First of all, assuming a pre-existing SIMD_WIDTH constant which contains our SIMD vector width, we can select an output region that covers all previous output rows, but only a number of columns that corresponds to an integer number of SIMD vectors:

use ndarray::s;

let [num_rows, num_cols] = start.shape();
let num_regular_cols = ((num_cols - 2) / SIMD_WIDTH) * SIMD_WIDTH;

let regular_output = s![1..(num_rows - 1), 1..=num_regular_cols];
let mut regular_out_u = end.u.slice_mut(regular_output);
let mut regular_out_v = end.v.slice_mut(regular_output);

let regular_input = s![0..num_rows, 0..=(num_regular_cols + 1)];
let regular_in_u = start.u.slice(regular_input);
let regular_in_v = start.v.slice(regular_input);

We can then iterate over rows of the output arrays and the corresponding windows of three consecutive input rows in the input arrays…

use ndarray::Axis;

let out_rows = (regular_out_u.rows_mut().into_iter()).zip(regular_out_v.rows_mut());

let in_windows = (regular_in_u.axis_windows(Axis(0), 3).into_iter())
    .zip(regular_in_v.axis_windows(Axis(0), 3));

// Cannot use `ndarray::azip` here because it does not support jointly
// iterating over ArrayViews of different dimensionality (here 1D and 2D)
for ((mut out_row_u, mut out_row_v), (win_u, win_v)) in out_rows.zip(in_windows) {
    // TODO: Process a row of output here
}

…and within that outer loop, we can have an inner loop on SIMD-sized chunks within each row of the output matrix, along with the corresponding input windows.

let out_chunks = (out_row_u.exact_chunks_mut(SIMD_WIDTH).into_iter())
    .zip(out_row_v.exact_chunks_mut(SIMD_WIDTH));

let in_windows = (win_u
    .axis_windows(Axis(1), SIMD_WIDTH + 2)
    .into_iter()
    .step_by(SIMD_WIDTH))
.zip(
    win_v
        .axis_windows(Axis(1), SIMD_WIDTH + 2)
        .into_iter()
        .step_by(SIMD_WIDTH),
);

// Cannot use `ndarray::azip` here for the same reason as before
for ((mut out_chunk_u, mut out_chunk_v), (win_u, win_v)) in out_chunks.zip(in_windows) {
    // TODO: Process a SIMD-sized chunk of output here
}

Finally, within the body of that inner loop, we can introduce a SIMD version of our regularized update algorithm, using std::simd:

use crate::data::Float;
use std::simd::prelude::*;

// Access the SIMD data corresponding to the center concentration
let simd_input = s![
    STENCIL_OFFSET[0],
    STENCIL_OFFSET[1]..SIMD_WIDTH + STENCIL_OFFSET[1],
];
let u = win_u.slice(simd_input);
let v = win_v.slice(simd_input);

// Load it as a SIMD vector
//
// The conversion from ArrayView to slice can fail if the data is
// not contiguous in memory. In this case, we know it should always
// be contiguous, so we can use unwrap() which panics otherwise.
type Vector = Simd<Float, SIMD_WIDTH>;
let u = Vector::from_slice(u.as_slice().unwrap());
let v = Vector::from_slice(v.as_slice().unwrap());

// Compute the diffusion gradient for U and V
let [full_u, full_v] = (win_u.windows([1, SIMD_WIDTH]).into_iter())
    .zip(win_v.windows([1, SIMD_WIDTH]))
    .zip(STENCIL_WEIGHTS.into_iter().flatten())
    .fold(
        [Vector::splat(0.); 2],
        |[acc_u, acc_v], ((stencil_u, stencil_v), weight)| {
            let stencil_u = Vector::from_slice(stencil_u.as_slice().unwrap());
            let stencil_v = Vector::from_slice(stencil_v.as_slice().unwrap());
            let weight = Vector::splat(weight);
            [
                acc_u + weight * (stencil_u - u),
                acc_v + weight * (stencil_v - v),
            ]
        },
    );

// Compute SIMD versions of all the float constants that we use
let diffusion_rate_u = Vector::splat(DIFFUSION_RATE_U);
let diffusion_rate_v = Vector::splat(DIFFUSION_RATE_V);
let feedrate = Vector::splat(opts.feedrate);
let killrate = Vector::splat(opts.killrate);
let deltat = Vector::splat(opts.deltat);
let ones = Vector::splat(1.0);

// Compute the output values of u and v
let uv_square = u * v * v;
let du = diffusion_rate_u * full_u - uv_square + feedrate * (ones - u);
let dv = diffusion_rate_v * full_v + uv_square - (feedrate + killrate) * v;
let out_u = u + du * deltat;
let out_v = v + dv * deltat;

// Store the output values of u and v
out_u.copy_to_slice(out_chunk_u.as_slice_mut().unwrap());
out_v.copy_to_slice(out_chunk_v.as_slice_mut().unwrap());

The main highlights here are that

• We can convert back from an ArrayView that has contiguous storage to a standard Rust slice for the purpose of interacting with the SIMD API, which doesn’t know about ndarray.
• We can still use 1D-like iteration in our inner diffusion gradient loop, it is only the outer loops on output elements that are affected by the change of algorithm.
• Floating point constants can be turned into SIMD vectors whose elements are all equal to the constant by using Simd::splat, which on x86 maps to the hardware broadcastss instruction.
• Adding SIMD to any nontrivial codebase without turning it into an unreadable mess is a major software engineering challenge¹.

Finally, because we are using the experimental nightly-only std::simd API, we will need to enable it by adding the associated #![feature(portable_simd)] directive to the top of exercises/src/lib.rs (assuming this is where you have put the update function’s implementation).

Exercise

Make a backup of your current update function, you will need some of it to handle the irregular subset of the data (simulation domain edges, extra columns that do not fit a SIMD vector nicely, etc).

Then integrate the above regularized SIMD algorithm into your code, and complete it by adding function multiversioning through the multiversion crate (as presented in the SIMD chapter), so that you get something to put inside of this SIMD_WIDTH constant:

const SIMD_WIDTH: usize = ...;

Finally, make your update function handle the irregular part of the simulation domain by reusing your former implementation.